PROPOSTA
D'interès per a: lingüistes, matemàtics, psicòlegs, pedagogs, ensenyants, científics i/o qualsevol persona que li agradi saber el per què de les coses.
QUÈ TENÍEM FINS AVUI?
Doncs fins avui tenim tot tipus de diccionaris (de la llengua, etimològics, ideològics, thesaurus, traductors, ...), enciclopèdies, també teníem recursos com categories, ..., taxons, merons, ... i darrerament revestiments informàtics com webs semàntiques, OWL (o WOL), ... Com si encara utilitzesim els números romans. Se suggereixen les breus i entretingudes lectures d'En Ferran "El meu amic Carles.pdf" (1999) 58 kB, sobre l'anacronisme de l'ordre alfabètic; i d'en Ramon "Sistema conceptual para no conceptuales" ("SistemaconceptualRB.pdf", 2009 367 kB) sobre l'exactitud de l'arbre.
EL SISTEMA CONCEPTUAL
L'ARBRE
La mateixa estructura arbrada dels nombres indo-aràbigs, que ha aportat resultats extraordinaris a la civilització humana (com la simple i potent representació de l'enorme quantitat 64 785 213),
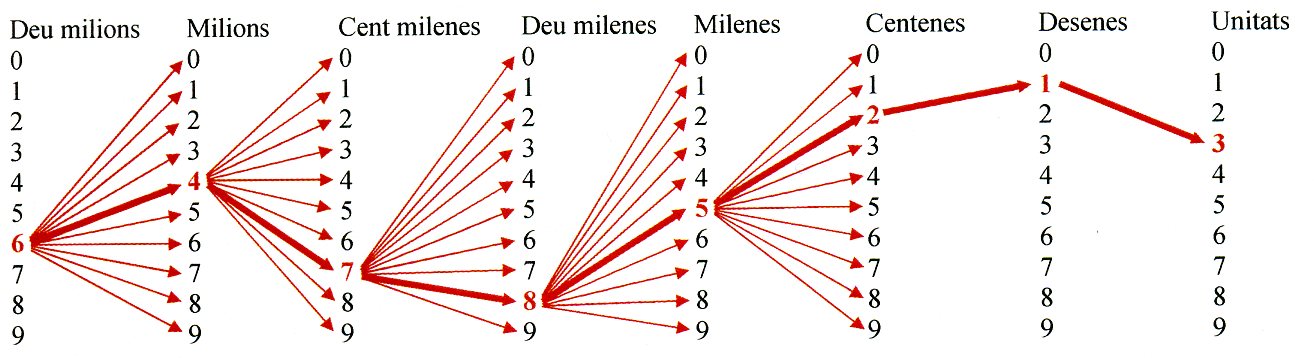
es pot utilitzar amb els conceptes en general, a diferència dels actuals criteris arbitraris, com els alfabètics o les categories dels thesaurus.
Com que els conceptes no són, ni de lluny, un conjunt tan simple com els nombres (caracteritzats aquests darrers, per la seva regular i monòtona sequencialitat) la metodologia estructural també és la de progressius nivells com els nombres (..., milers, centenes, desenes, unitats, dècimes, ...), però els seus criteris de construcció (un algoritme algebraic anomenat “Successió algebraica exacta curta” [“SAEC”] que no li cal conèixer al lector) són més complexos/ laboriosos.
PORFIRI (s. III) va estar a pocs passos de trobar un sistema igualment exacte que la numeració indo-aràbiga, però de més gran abast, és a dir, per a tots els conceptes. Tot i la progressiva i reeixida implantació dels sistemes numèrics posicionals en els darrers 200 anys, ni lingüistes ni matemàtics han donat el pas fins avui. No s’ha aprofitat el “miracle” dels sistemes numèrics*.
* Veure “KRÖNECKER i el miracle dels sistemes numèrics” [.170] a “Conscienciacio”
En els sistemes numèrics el criteri de partició de la “SAEC” és fix, les “classes de restes mòdul 10” (o “classes de restes mòdul 2” en el sistema binari/ digital), el que origina la inductivitat que caracteritza els números (allò del +1). En lloc d’això, en el “Sistema conceptual” el criteri de partició és qualsevol altre concepte.
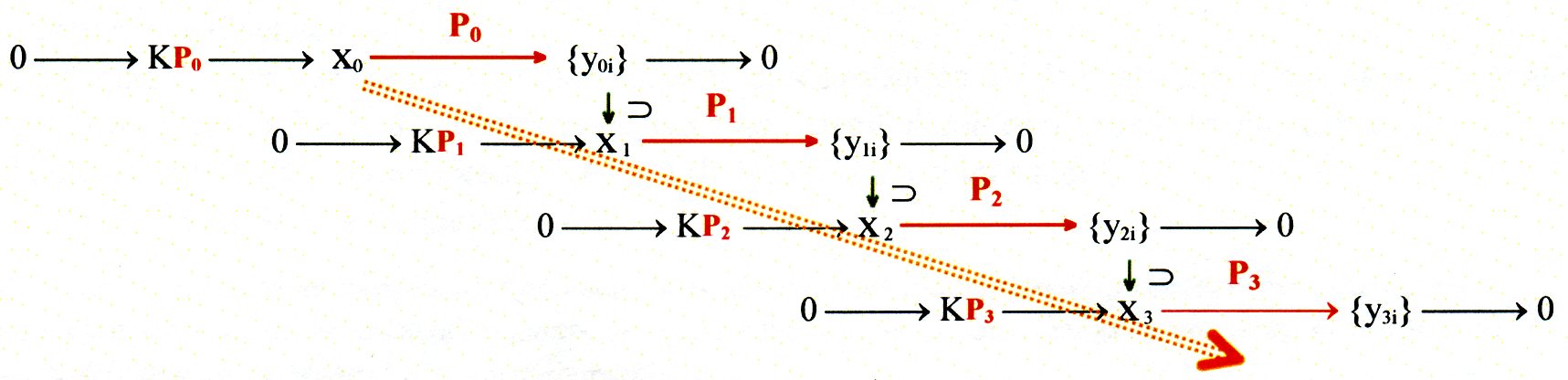
Aquest esquema representa matemàticament el procés constructiu. En la "SAEC" de la primera línia, cada una de les classes d'equivalència "y01", "y02", "y03", ... del conjunt {y0i} genera una nova "SAEC" que es representa en la línia següent (x1 € {y0i}, o x1 està inclòs en {y0i} si es té en compta que són continguts conceptuals). Així, la fletxa diagonal vermella és una de les moltes possibles línies de descendents que es generen.
Al concepte utilitzat en cada cas com a criteri de partició li direm “padrastre” (el concepte de partida és la “mare” i el resultat són els conceptes “fills” de la parella, tot el que forma una “família” de conceptes més específics).





en espiral, espiral barrada, lenticular, el·líptica, irregular, ...;
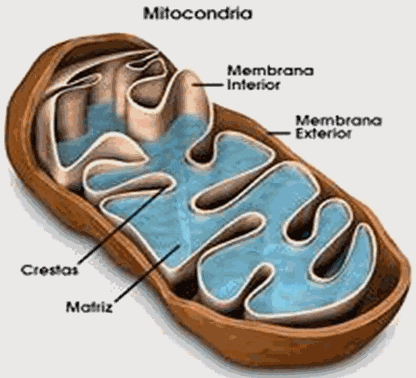

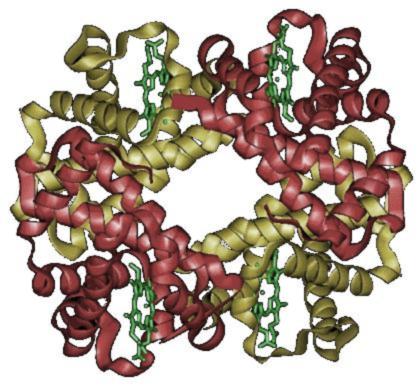
membranosa, fibrilar, globulina, ...;
¿Qui podia pensar que galàxia, proteïna, temperament, hidrocarbur o virus generen conceptes "fill" relacionats? El Sistema conceptual explicita/ consciència exhaustivament tota la relacionabilitat. I la relacionabilitat és el que permet la transferència en l’aprenentatge i la comprensió.
El padrastre aporta automàticament les característiques distintives entre els fills generats (“Kernel”), és a dir, aporta les afegides abstraccions/ adjectius, així com les característiques de la família en el seu conjunt (“CoKernel”).
CoKernel: els conjunts dels tipus de galàxies en espiral, de disc, lenticulars, ... es caracteritzen per les seves corresponents formes específiques.
Encara més, hi ha “poligàmia” (quelcom implantejable en els nombres però obligat en els conceptes per la seva prolífica relacionabilitat i la característica d’ “herència múltiple”): un mateix concepte, la “mare”, pot generar diverses famílies diferents amb els corresponents “padrastres” ("a", "b", "c", "d", ...) i “fills” diferents.
b) Mamífers [segons alimentació] ⇒ Mamífers carnívors, herbívors o omnívors
c) Mamífers [segons subClasse] ⇒ Mamífers prototeris o teris
d) Mamífers [segons Ordre] ⇒ Mamífers monotremes, marsupials, insectívors, ..., artiodàctils o primats
e) etc., etc., etc.
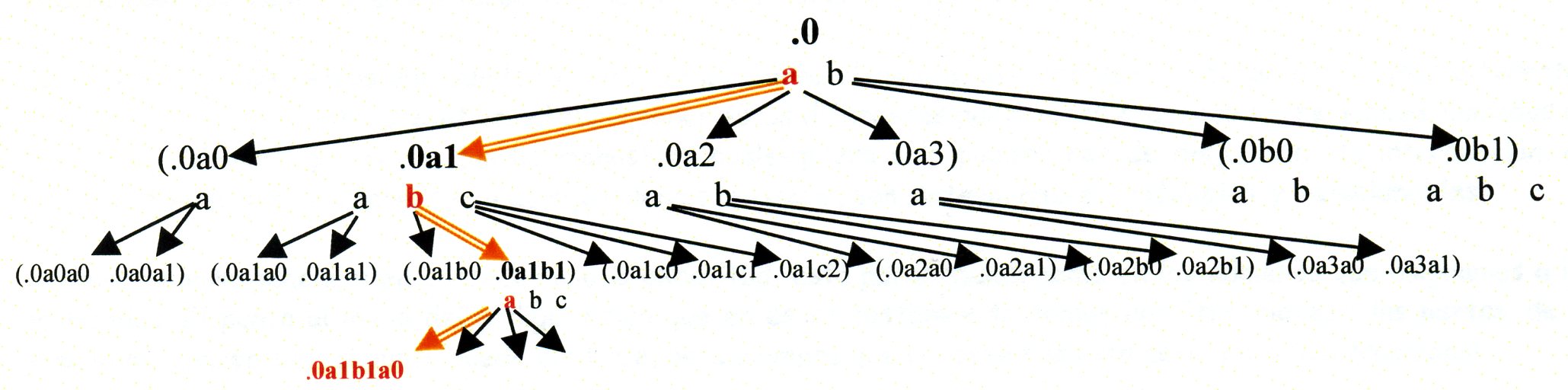
Si en l'esquema anterior es representava una sola línia de descendents segons el seu procés algebraic de generació, aquí apareix el resultat global: totes les línies de descendents però sense aquestos processos. És el primer arbre del "Sistema conceptual", l' "Arbre intrínsec i exacta dels conceptes".
La inductivitat i la relació de multiplicitat (10, 2, ... segons la base dels sistema numèric) dels números és substituïda en els conceptes en general per les relacions conceptuals vinculades al padrastre, per la contigüitat i per la compacitat (que originen la corresponent topologia).
Els “fills” estan ben definits (per la construcció matemàtica associada), pertanyent a una sola de les classes d’equivalència.
Per tot això, l’arbre intrínsec dels conceptes és més prolífic que l’arbre dels sistemes numèrics, i en lloc d’una superfície per a representar-lo (veure més a munt l’arbre associat al número 64 785 213), ens cal un espai tridimensional, com si es tractés d’un arbre real.
L’important és garantir l’exactitud, en aquest cas aportada per les corresponents “Successions algebraiques exactes curtes” [SAEC]. No podem fer el que ens sembli millor o més còmode, com s’ha fet sempre fins avui (com es fa amb amb les enciclopèdies, amb els diccionaris de la llengua, amb els de sinònims, amb les “Categories”, amb els “Taxons”, amb les “Ontologies”, amb els “Mapes mentals”, etc...). La dificultat és doble (però a la vegada, de doble utilitat):
LA PARTICIÓ INTRÍNSECA (Els conceptes més genèrics/ universals i intrínsecs amb la nostra ment)
- Conceptes sensitius [Nivell estructural 1]:
- Conceptes sensitius estàtics (“Matèria”), a partir de l’any del nadó i dels signes lingüístics;
- Conceptes no sensitius (=Conceptes virtuals, compostos lingüísticament ["psicologia operatòria"]):
B) Cal seguir les regles constructives citades (criteris intrínsecs), de les que es deriven totes les propietats de l’estructura: l’exactitud ja esmentada, però, també, la representativitat i la simulabilitat (és a dir, la possibilitat de gestió amb l’ordinador) i, finalment, la relacionabilitat global.
LA RELACIONABILITAT: ELS RECURSOS MÉS POTENTS
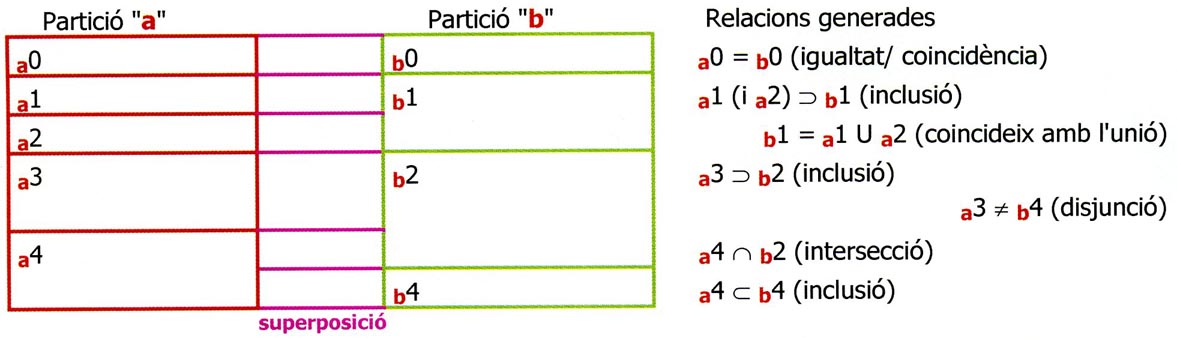
Ja tenim relacions com les esmentades: jeràrquiques, del padrastre, i booleanes. Però encara és molt més important afegir l’establiment de relacions entre dos conceptes qualssevol (i el lector ha de saber que dos conceptes correctament relacionats sempre generen un coneixement simple). Aquesta nova relacionabilitat es pot fer utilitzant relacions, o inclús conceptes normals degudament transformats en relacions per la relació "estrella" ("Star operator", veure "Dualitat algebraica").
Amb les relacions estem superposant a l’arbre de conceptes exactes una teranyina multicolor que suposa innombrables coneixements perfectament representats i, pel mateix motiu, gestionables (recuperables, operables, ...). Apareix l’ “Espai cognitiu” per on l’aprenentatge esdevé una simple i gratificant navegació.
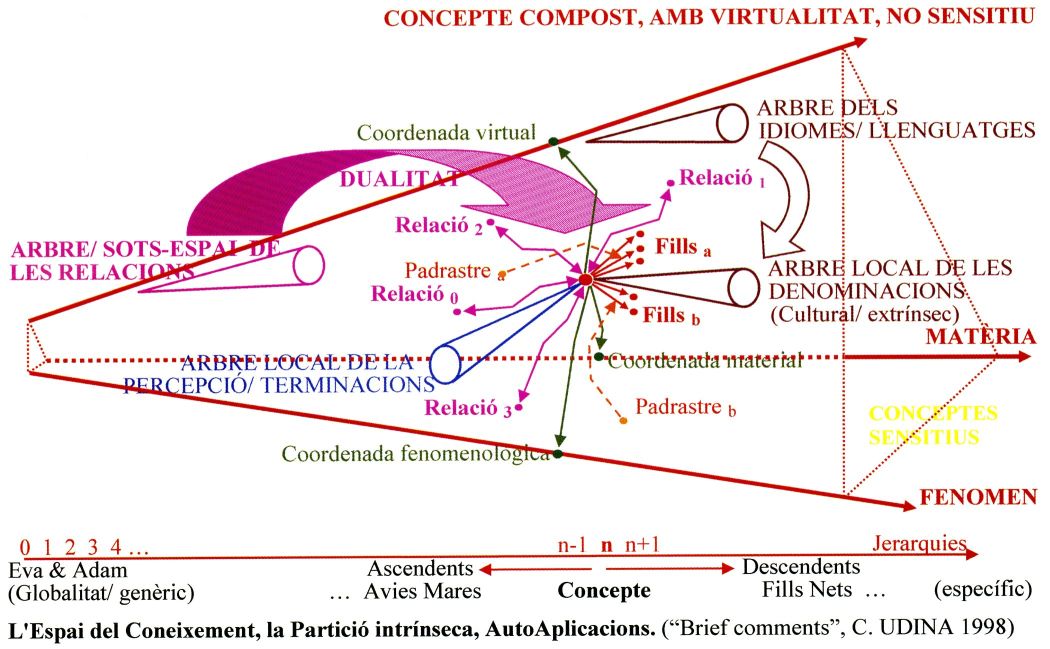
Veure "Breves comentarios" (1999) 85 kB i també "L'arbre de la saviesa.pdf" 221 kB
Cada concepte esdevé un mapa conceptual, però intrínsec, amb tots els coneixements associats i la possibilitat de navegar a través de les relacions intrínseques que defineixen aquets coneixements.
Com en qualsevol procés: la disciplina d’observar una metodologia adient porta a un resultat útil/ aplicable.
Amb un sistema conceptual es fa trivial diferenciar –per a emprar-los correctament– conceptes pròxims (finesa/ sensibilitat) com “Programa”, “Projecte” o “Planificació”. Veure "Programa projecte planificació.pdf".
Escriure be, comprensiblement, evitant textos ambigus es tan fàcil amb un Sistema conceptual com l’ús d’un corrector ortogràfic. Veure "Aplicacions als Hipertextos comprensius i correctors del contingut del text".
Amb un Sistema conceptual, la traducció a qualsevol idioma és automàtica perquè es redueix a la correcta referenciació del text a l’esmentat sistema (que només ha de tenir referenciats els diccionaris dels dos idiomes). Veure "Aplicacions a la Traducció automatica".
REFLEXIÓ FINAL I EXPECTATIVES
l’actual “sistema” lingüístic al Sistema conceptual,
seria similar a passar de la utilització dels
números romans als números aràbics.
Fa 200 anys, amb la “socialització” (la implantació arreu) dels sistemes numèrics posicionals (decimal, ...) ningú podia imaginar l’espectacular desenvolupament que suposarien per a la matemàtica, per a la ciència, per a la tecnologia, per a l’economia (globalització), per a la informàtica (sistema numèric posicional binari), ... que ha estat possible per la seva exactitud i intuïtivitat.
Tanmateix, avui és inimaginable el que pot suposar l’extensió a tots els conceptes d’una anàloga representació exacta i intuïtiva (intrínseca). És lògic, doncs, que sorprengui la seva possible aplicació a àmbits tan distants com la genètica (veure "Aplicacions a la bioquímica i la genètica") o la mecànica quàntica ("Aplicacions a la Mecànica quàntica").
En el primer cas és fins i tot de sentit comú: la codificació genètica és una estructura de sistemes del tipus (+M, +S), molt més simple que les del tipus (-M, +S) de la psique. A més a més, les codificacions de la psique es deriven de la codificació genètica. En conseqüència qualsevol estructura/ característica de la codificació genètica és segur que també està present a la psique. Per tot això, el coneixement de les darreres, les psíquiques, pot aportar informació de les primeres, les genètiques.
En el cas de la mecànica quàntica, la complexitat i el desconcert que estan produint els fenòmens que es van coneixent fa que, dia a dia, s'obrin més interrogants que explicacions: “Hace falta una teoria que hoy no podemos ni imaginar” (A. J. LEGGETT), “Le mystère des origines de l’Univers est loin d’être résolu” (G. SMOOT). “Teoria inimaginable” o “solució al misteri” que per un seguit d’indicis podria ser aportada per una estructura informacional del tipus (-M, +S).